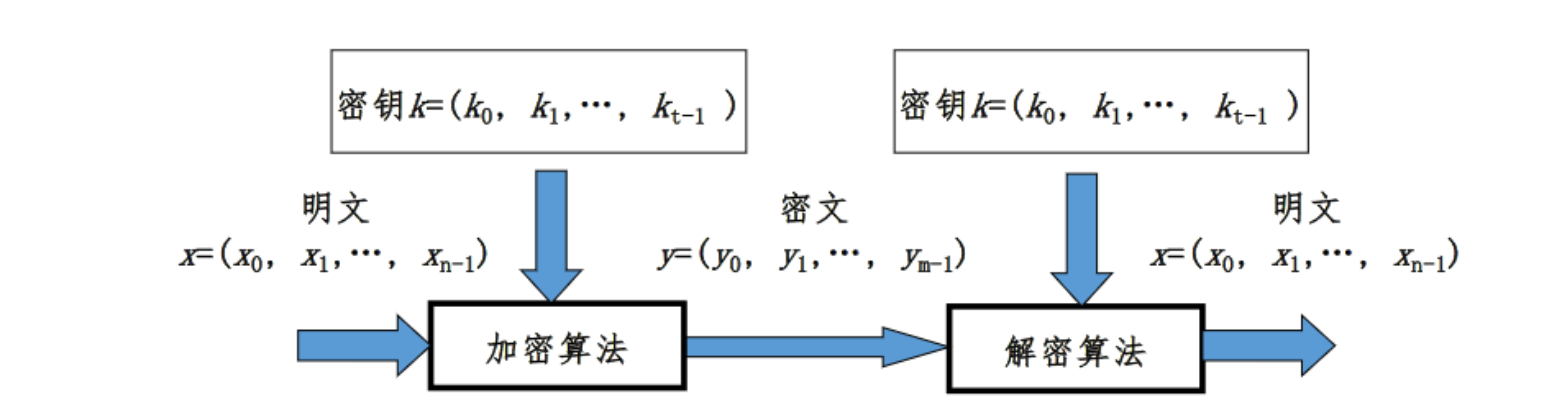
第一章 引言
信息安全基本属性
- 机密性 (Confidentiality)
保证信息为授权者使用而不泄漏给未经授权者。
别人“看不到”或“看不懂” - 认证(Authentication)
消息认证,保证消息来源的真实性
身份认证,确保通信实体的真实性
证明“你就是你” - 完整性 (Integrity)
数据完整性,未被未授权篡改或者损坏
系统完整性,系统未被非授权操纵,按既定的功能运行
信息没有被“动过” - 不可否认性(Non-repudiation )
要求无论发送方还是接收方都不能抵赖所进行的传输 - 可靠性(Reliability)
特定行为和结果的一致性 - 可用性 (Availability)
保证信息和信息系统随时为授权者提供服务,而不要出现非授权者滥用却对授权者拒绝服务的情况。 - 可控性(Controllability)
授权实体可以控制信息系统和信息使用的特性 - 审计(Accountability)
确保实体的活动可被跟踪
密码编码学
密码算法的分类
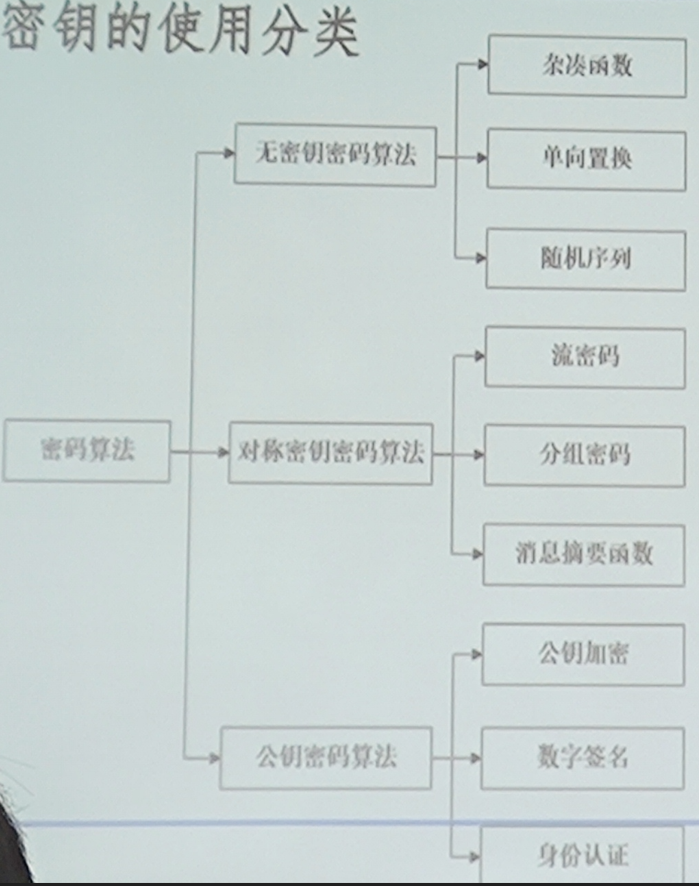
按功能
加密算法:用于机密性解决方案
杂凑函数:用于完整性解决方案
数字签名:用于认证和不可否认性
按密钥的使用方式
对称密钥密码 : 加密密钥与解密密钥相同
非对称密钥密码(公钥密码):加密密钥与解密密钥不同
公钥密码部分解决了对称密钥密码算法中密钥共享、密钥管理的问题。
第一代公开的、完全说明细节的商业级密码标准是DES
被动攻击与主动攻击
被动攻击->不影响通讯
网络嗅探、流量分析
主动攻击->影响通讯
网络中断、假冒身份、数据包篡改
密码分析学
安全的概念
Kerckhoffs假设
假定密码分析者和敌手知道所使用的密码系统。 即密码体制的安全性仅依赖于对密钥的保密,而不应依赖于算法的保密。
密码分析学的目标
- 破译密文
- 破译密钥
- 破译出明文
密文是[破译]的基础,密钥是[破译]的核心目标,而明文虽然是有用的想要的信息,但它是[破译出]密钥后才有的产物,所以核心是破译密文和密钥
密码分析方法的分类
攻击密码体制的方法
- 穷举攻击:通过试遍所有的密钥来进行破译。
对抗:可增大密钥的数量。 - 统计分析攻击:通过分析密文和明文的统计规律来破译。
对抗:设法使明文和密文的统计规律不一样。 - 解密变换攻击:针对加密变换的数学基础,通过数学求解设法找到解密变换。
对抗:选用具有坚实的数学基础和足够复杂的加密算法。
密码破译
唯密文攻击(Ciphertext Only Attack):在唯密文攻击中,攻击者只能获取到加密后的密文,没有任何关于明文或密钥的其他信息。攻击者的目标是通过分析密文来推断出明文或密钥的信息。
已知明文攻击(Known Plaintext Attack):在已知明文攻击中,攻击者可以获取到一些已知明文和对应的密文对。攻击者的目标是通过这些已知对来破解密钥或加密算法。
选择明文攻击(Chosen Plaintext Attack):在选择明文攻击中,攻击者可以选择一些明文,并获取对应的密文。攻击者可以根据这些选择的明文和对应的密文来分析加密算法或破解密钥。
选择密文攻击(Chosen Ciphertext Attack):在选择密文攻击中,攻击者可以选择一些密文,并获取对应的解密结果或其他与密文相关的信息。攻击者可以利用这些选择的密文和相关信息来破解密钥或分析加密算法。
以上攻击强度依次递增
无条件安全和计算上安全
无条件安全的(不可破译的)
无论截获多少密文,都没有足够信息来唯一确定明文,则该密码是无条件安全的,即对算法的破译不比猜测有优势
计算上安全的
使用有限资源对一个密码系统进行分析而未能破译,则该密码是强的或计算上安全的
计算上安全的密码算法要满足的准则
- 破译密文的代价超过被加密信息的价值。
- 破译密文所花的时间超过信息的有用期。
习题
Kerckhoffs假设指的是?
密码分析的目标在于?
古典密码算法
置换密码
置换(Permutation)
对明文字符或字符组进行位置移动的密码
明文的字母保持相同,但顺序被打乱了。
值不变顺序变
单表代替密码算法
代替(Substitution)
密码构造一个或多个密文字母表,然后用密文 字母表中的字母或者字母组来代替明文字母或字母组,各字母或 字母组的相对位置不变,但其本身的值改变了。
值变顺序不变
加法密码
凯撒密码
乘法密码
仿射密码
仿射密码是乘法密码和加法密码的结合。
加密函数:y=ax+b(mod26)
密钥:a,b
解密函数:x=a^(-1)(y-b)(mod26)缺点:不能对抗统计分析
多表代替密码算法
Vigenere(维吉尼亚)密码
可证明安全性
密码游戏与规约
把密码破译归结到困难问题上,而当困难问题实际上是简单的:
- 密码不安全,可通过解决困难问题来攻破
- 密码还是安全的,但是不是可证明安全
CDH假设

第二章 流密码
基本概念
一次一密
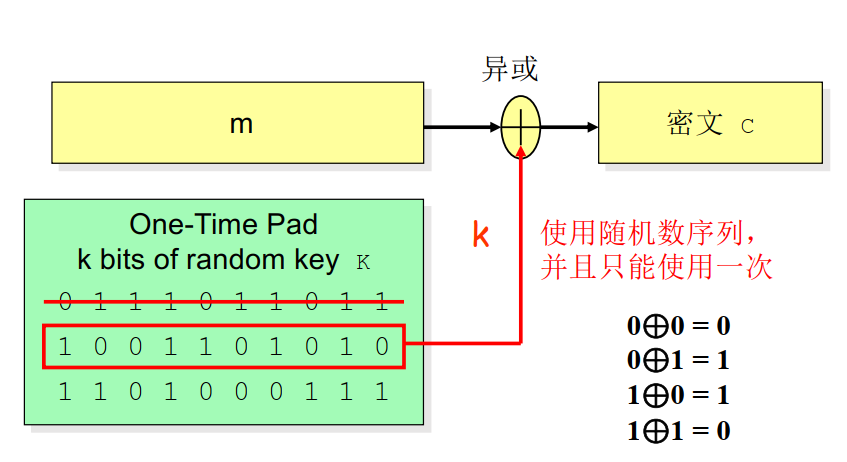
• 优点:
• 密钥随机产生,仅使用一次
• 无条件安全
• 加密和解密为加法运算,效率较高
• 缺点:
• 密钥长度至少与明文长度一样长
• 密钥共享困难,不太实用
• 改进:
• 种子密钥生成无限长的密钥(流密码的思想,共享一小段)
流密码的基本思想
• 利用密钥k产生一个密钥流z=z0z1z2…,并使用如下规则对明文串
x=x0x1x2…(加法或者简单处理方法)加密:
y=y0y1y2…=Ez0(x0)Ez1(x1) Ez2(x2)…,
流密码的定义
内部记忆元件的状态σi独立于明文字符的叫做同步流密码,否则叫
做自同步流密码。
在同步流密码中,由于zi=f(k,σi)与明文字符无关,因而此时密文字符yi=Ezi(xi)也不依赖于此前的明文字符。
可将同步流密码的加密器分成密钥流产生器和加密变换器两个部分。
同步流密码

密码设计者的最大愿望是设计出一个滚动密钥生成器,使得密钥经其扩展成的密钥流序列具有如下性质:
极大的周期
良好的统计特性
抗线性分析
有限状态自动机模型
有限状态自动机可用有向图表示,称为转移图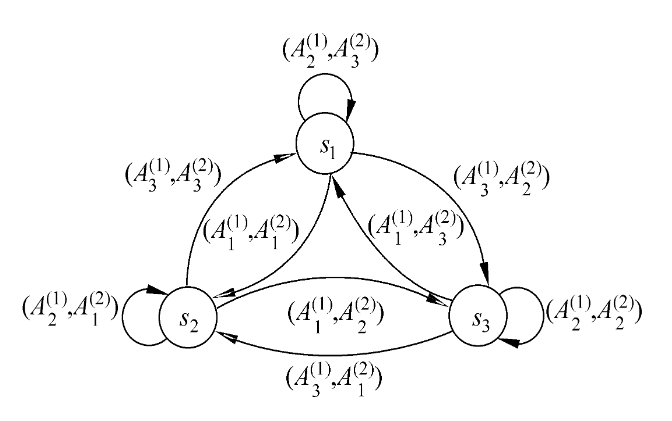
箭头和箭尾代表状态,()中前者代表引起状态改变的输入,后者代表状态改变后的输出
密钥流生成器
密钥流产生器: 参数为k的有限状态自动机,
一个输出符号集Z、一个状态集∑、两个函数φ和ψ以及一个初始状态σ0组成。
状态转移函数φ:σi→σi+1,将当前状态σi变为一个新状态σi+1,
输出函数ψ:σi→zi,当前状态σi变为输出符号集中的一个元素zi。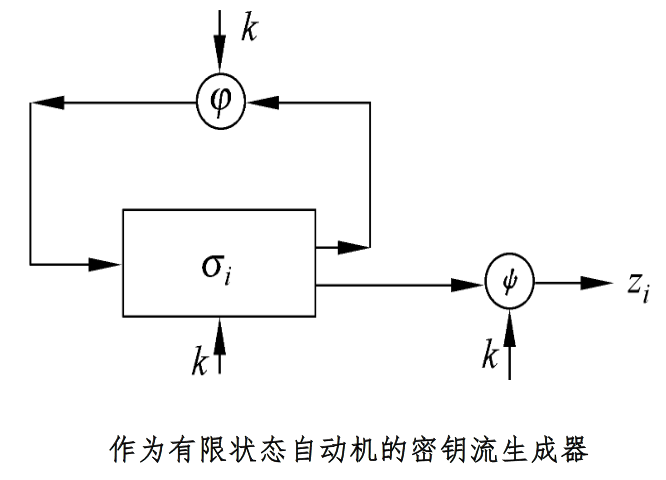
一般采用线性的φ和非线性的ψ
密钥流生成器可分成驱动部分和非线性组合部分
驱动部分是一个或多个线性反馈 移位寄存器。(LFSR是流密码构造的关键模块)
二元序列的伪随机性
二元序列的相关概念
GF(2)上的一个无限序列->a=(a1,a2,…,an,…)称为二元序列,若 ai属于GF(2),0或者1。
游程
自相关函数
伪随机序列满足条件
Golomb伪随机公设
线性反馈移位寄存器
反馈移位寄存器
GF(2)上一个n级反馈移位寄存器由n个二元存储器与一个反馈函数f(a1,a2,…,an) 组成
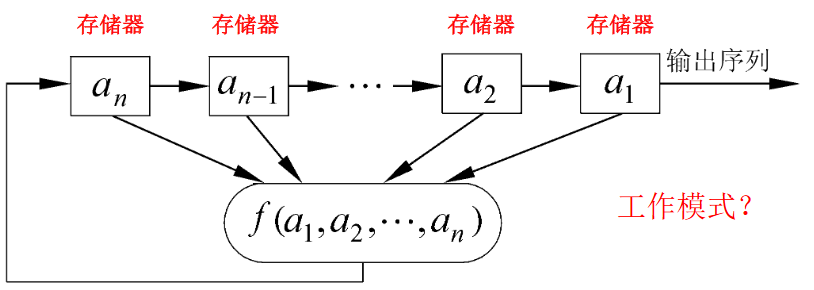
反馈函数f(a1,a2,…,an)是n元布尔函数,即函数的自变量和因变量只取0和1这 两个可能的值。
线性反馈移位寄存器
反馈函数是个线性函数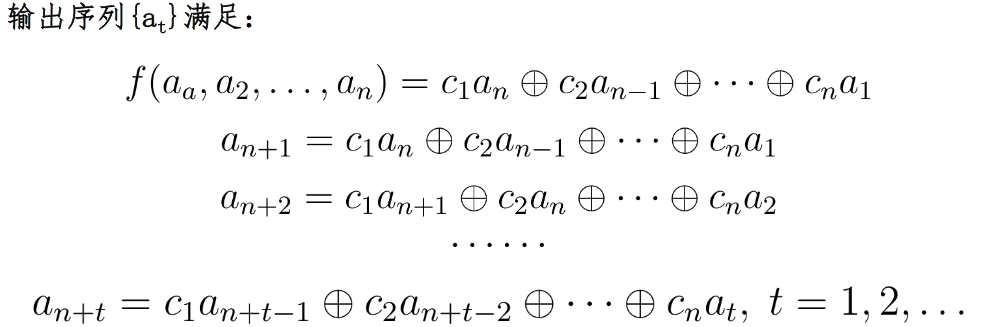
密钥流的周期
给定密钥流 ,如果存在整数r,使得 对于任意 ,都有 ,则称 r为该密钥流的一个周期, 称满足 的最小正整数为该密钥流的最小周期或简称周期。
m-序列
线性反馈移位寄存器的多项式表示
定理2.2 p(x)|q(x)的充要条件是G(p(x)) Í G(q(x))
m-序列产生的条件
Golomb伪随机公设
①在序列的一个周期内,0与1的个数相差至多为1。
②在序列的一个周期内,长为i的游程占游程总数的1/2i (i=1,2,…),且在等长的游程中0的游程个数和1的游程个数相等。
③异相自相关函数是一个常数。
m-序列安全性
解方程方法
线性反馈移位寄存器综合求解法
非线性序列
密钥流生成器可分解为驱动子系统和非线性组合子系统
驱动子系统常用一个或多个线性反馈移位寄存器来实现
非线性组合子系统用非线性组合函数F来实现
密钥k扩展 而成的密钥流序列z应满足的性质:
- 种子密钥的长度足够长(一般来说就是流密码的密钥长度)
- 极大的周期
- 良好的统计特性
- 极大的线性复杂度
- 极大的k错线性复杂度
- 抗统计分析
- 混乱性
- 扩散性
- 抗线性分析
Geffe序列生成器
J-K触发器
Pless生成器
第三章 分组密码
概述
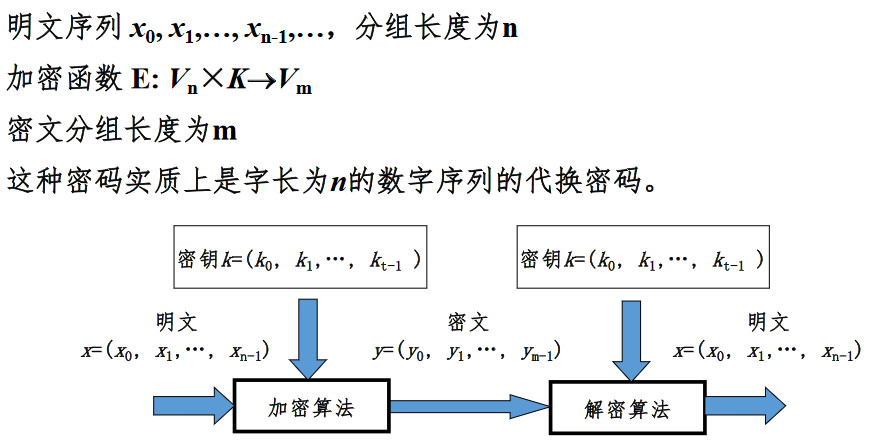
通常取n=m
若n<m ,则为有数据扩展的分组密码。
若n>m ,则为有数据压缩的分组密码。
安全性设计原则
混淆原则(Confusion)
- 混淆原则就是将密文、明文、密钥三者之间的统计关系和代数关系变 得尽可能复杂,使得敌手即使获得了密文和明文,也无法求出密钥的任何信息
- 即使获得了密文和明文的统计规律,也无法求出明文的新的信息
- 明文不能由已知的明文,密文及少许密钥比特代数地或统计地表示出来。
- 密钥不能由已知的明文,密文及少许密钥比特代数地或统计地表 示出来。
引入了非线性变化
扩散原则(Diffusion)
- 扩散原则就是应将明文的统计规律和结构规律散射到相当长的一段统计中去(Shannon的原话)
- 也就是说让明文中的每一位影响密文中的尽可能多的位,或者说让密 文中的每一位都受到明文中的尽可能多位的影响。
实际上扩散原则应该把密文和密钥的关系加进去,也就是要让密文中的每 一位影响尽可能多的位
分组密码算法的要求
- 分组长度n要足够大
防止明文穷举攻击 - 密钥量要足够大
使所有密钥同等地好+防止密钥穷举攻击 - 由密钥确定置换的算法要足够复杂
充分实现明文与密钥的扩散和混淆,没有简单的关系可循 - 加密和解密运算简单
易于高速实现 - 数据扩展
- 差错传播尽可能地小
一个密文分组的错误尽可能少的影响其他密文分组的解密
分组密码的结构
两种常见的分组密码结构是Feistel网络Feistel Net和 SP网络Substitution-permutation Net
DES->Feistal
AES->SP
代换
代换是输入集A到输出A’上的一一映射
双射条件保证在给定k下可从密文惟一地恢复出原明文
Feistel密码结构
乘积密码指顺序地执行两个或多个基本密码系统,使得最后结果的密码强度高于每个基本密码系统产生的结果
参数
分组大小
密钥大小
轮数
子密钥产生算法
轮函数
要求
快速的软件实现
算法容易分析
Feistel加密结构
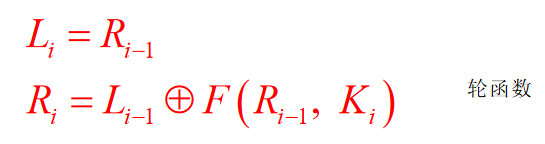
将每组明文分成左右两半L0和R0,在进行完n轮迭代后,左右两半再合并到一起以产生密文分组
其中Ki是第i轮用的子密钥,由加密密钥K得到。一般地,各轮子密钥彼此不同而且与K也不同
Feistel解密结构
本质上和加密过程是一样的,子密钥Ki的次序与加密过程相反
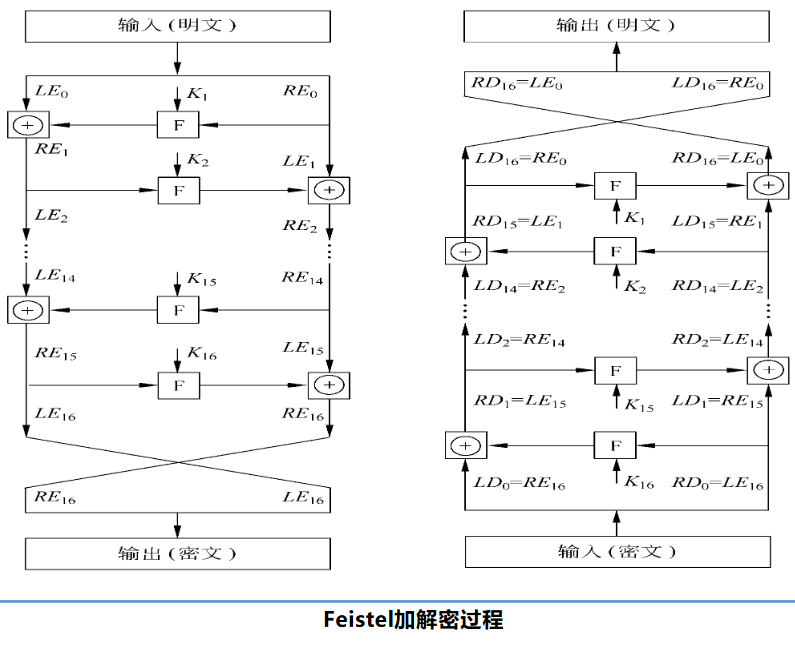
DES算法
基本参数
分组长度为64 bits (8 bytes)
密文分组长度也是64 bits
密钥长度为64 bits,有8 bits奇偶校验,有效密钥长度为56 bits
流程
初值置换IP
16轮迭代的乘积变换
逆初值置换IP^-1
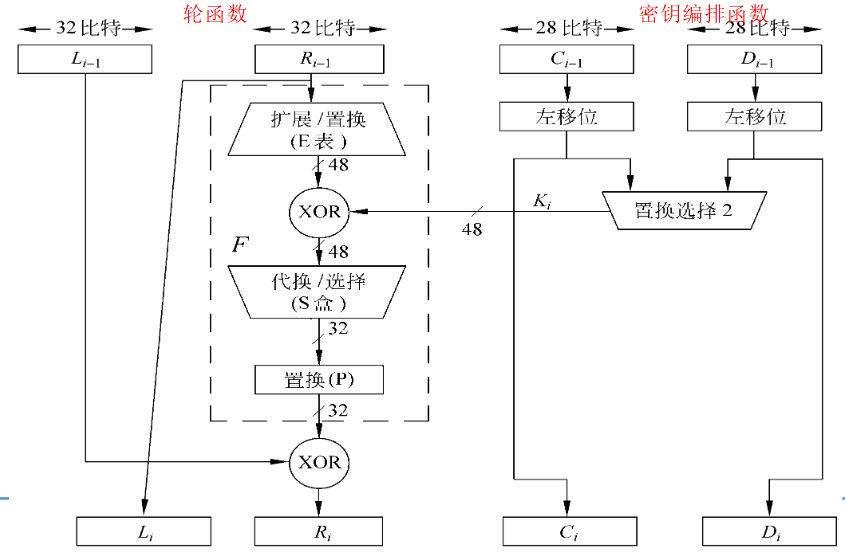
轮函数
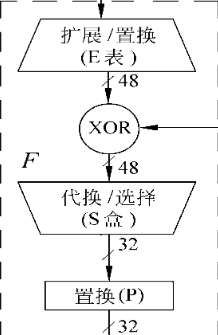
即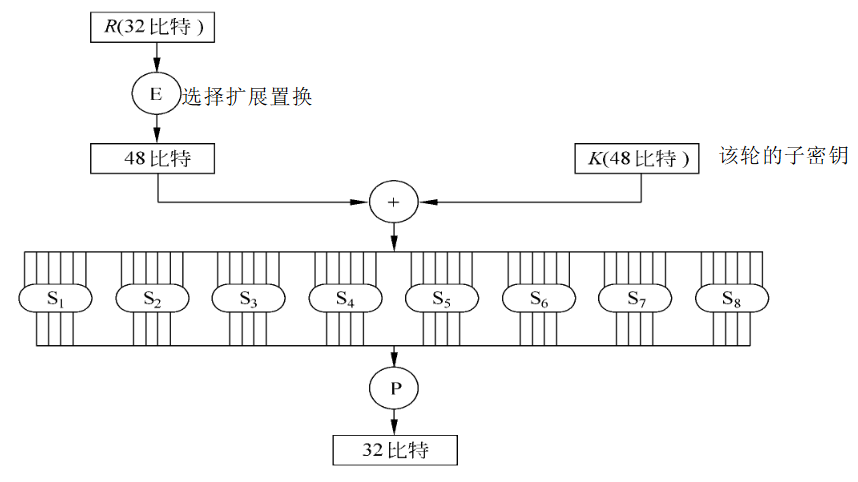
密钥编排
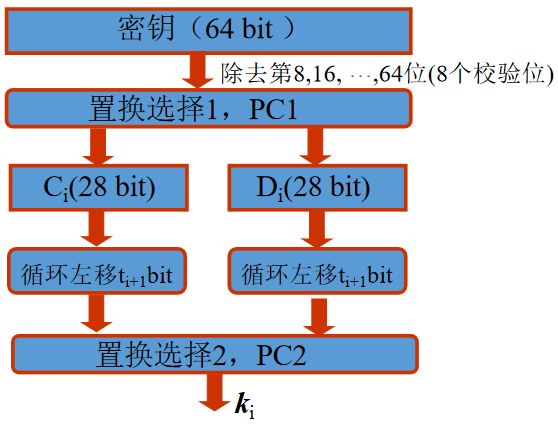
即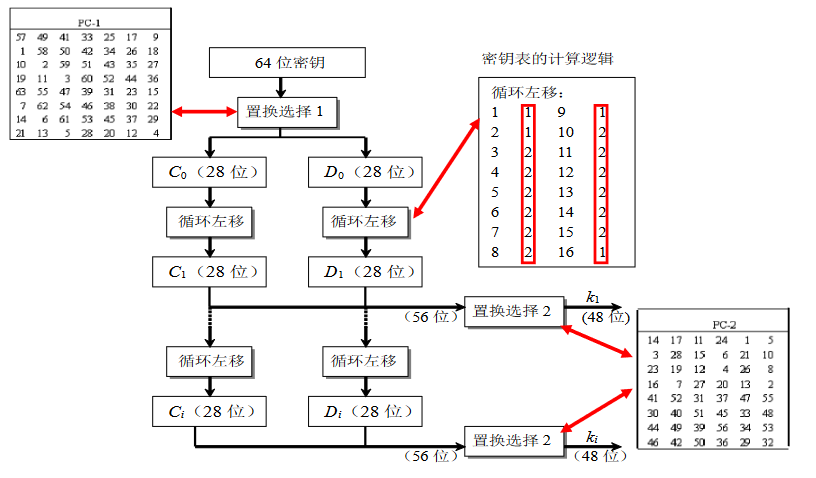
填充Padding
给定加密消息的长度是随机的,按64bit分组时,最后一组消息 长度可能不足64 bit。可以填充一些数字,通常用最后1字节作为填 充指示符(PI)
DES的安全性
目前攻击DES的主要方法有时间-空间权衡攻击、差分攻击、线性攻击和相关 密钥攻击等方法
线性攻击方法是最有效的一种方法
多重DES
多重DES就是使用多个密钥利用DES对明文进行多次加密
可以增加密钥量
双重DES
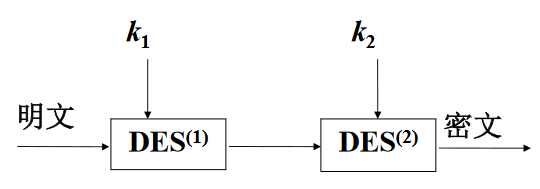
中间相遇攻击
三重DES
当k1=k3时,则称为双密钥三重DES
分组密码的工作模式
- 工作模式:根据不同的数据格式和安全性要求, 以一个具体的分组密码算法为基础构造一个分组密码系统的方法
电码本(ECB)模式
- 直接利用加密算法分别对分组数据组加密
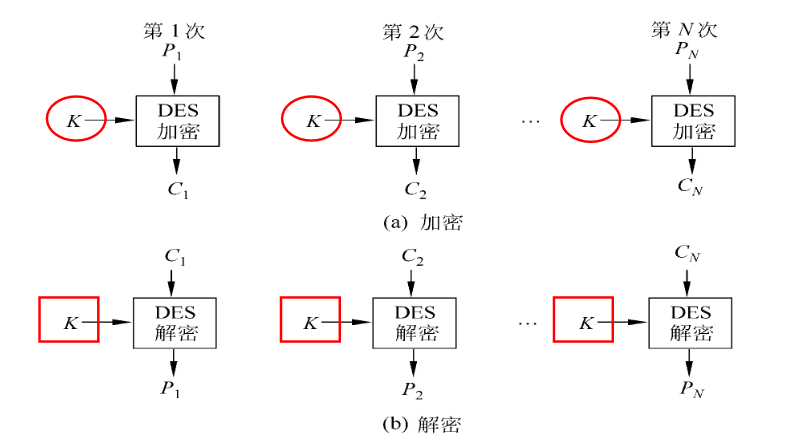
优点:
(1)实现简单;
(2)不同明文分组的加密可并行实施,尤其是硬件实现时速度很快
缺点:
(1)相同明文分组对应相同密文分组
(2)不能隐蔽明文分组的统计规律和结构规律,不能抵抗统计分析、重传和代换攻击
密码分组链接(CBC)模式
- 这种模式先将明文分组与上一次的密文块进行按比特异或,然后再进行加密处理
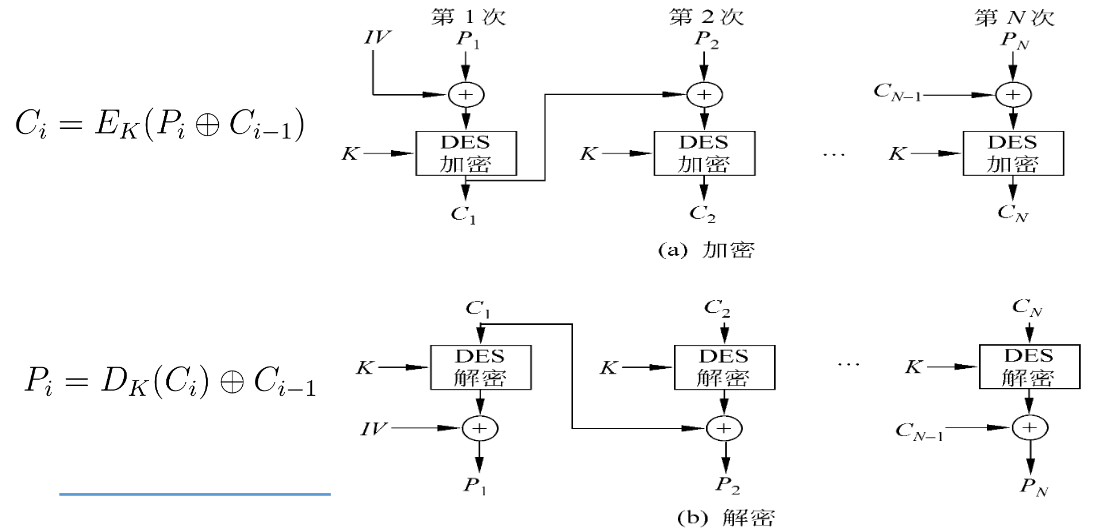
特点:
- 明文块的统计特性得到了隐蔽->各密文块不仅与当前明文块有关,而且还与以前的 明文块及初始化向量有关
- 具有有限的错误传播特性(两步)->一个密文块的错误将导致两个密文块不能正确解密
- 具有自同步功能->密文出现丢块和错块不影响后续密文块的解密
密码反馈(CFB)模式
若待加密消息需按字符、字节或比特处理时,可采用CFB模式。 并称待加密消息按 r 比特处理的CFB模式为 r 比特CFB模式
- 选取最左边的r比特 作为加密密钥
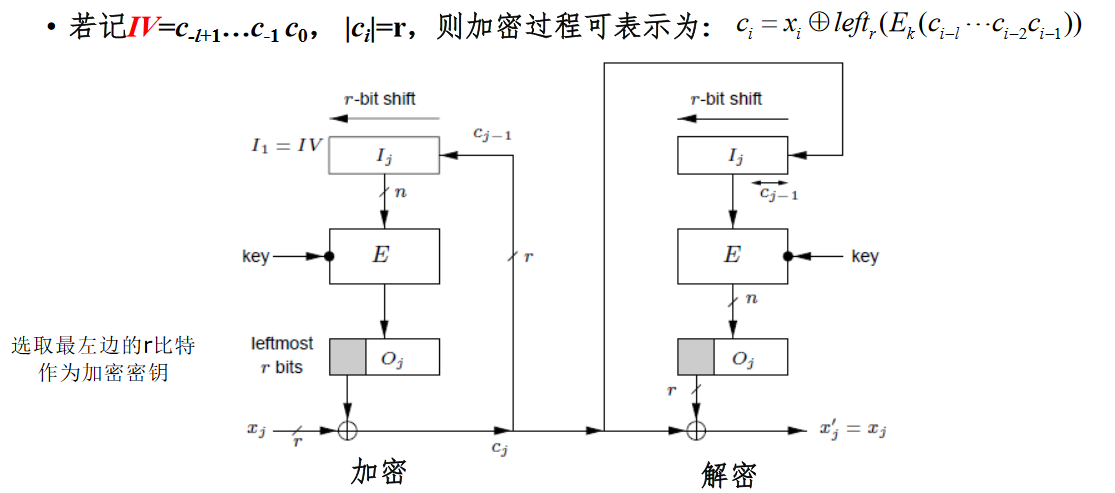
特点
- 相同明文(改变IV同样会导致相同的明文输入得到不同的加密 输出。IV无需保密
- 链接依赖性(链接机制致使密文组依赖于当前明文组和其前面的明文组,重排密文组会影响解密
- 错误的传播(一个或多个比特错误出现在任一个r比特的密文组中
- 错误恢复(自同步
输出反馈(OFB)模式
OFB模式在结构上类似于CFB模式,但反馈的内容是DES的输出而不是密文!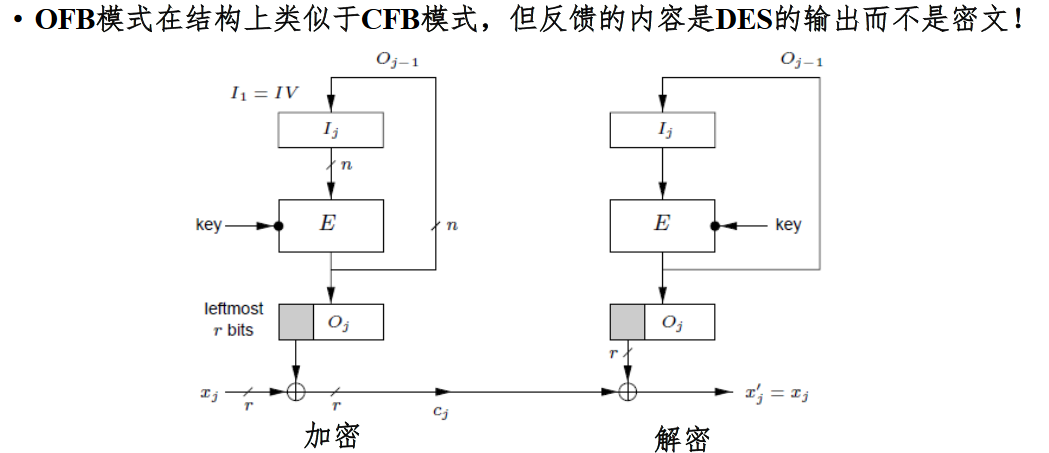
特点:
- 相同明文(改变IV同样会导致相同的明文输入得到不同的加密 输出
- 没有链接依赖性(密钥流是独立于明文的
- 没有错误传播(有一个或多个比特错误的任一密文字符仅会影响 该字符的解密
- 错误恢复(OFB模式能从密文比特错误中得以恢复,但在丢失密文 比特后就无法实现自同步了,这是因为丢失密文比特会破坏密钥流 的编排
计数器(CTR)模式
(OFB模式的简化版本)
结构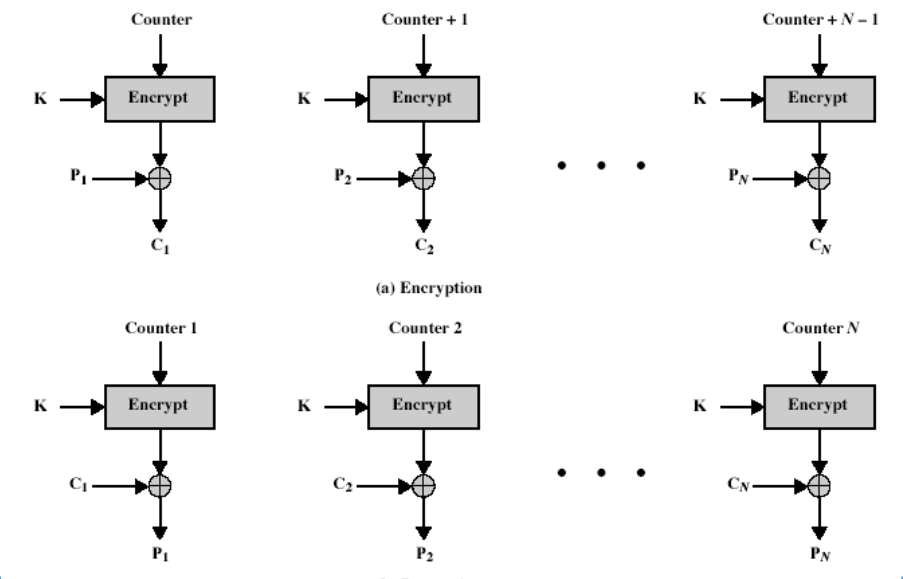
优点:
- 效率(可并行加密、预处理、吞吐量仅受可使用并行数量的限制
- 加密数据块的随机访问
- 可证明安全
- 简单性(只要求实现加密算法
前四类工作模式比较和选用
- ECB模式简单、高速,但最弱,易受重放和替换攻击,一般用于加密长度小于等于分组长度的消息。
- 明文不易丢信号,对明文的格式没有特殊要求的环境可选用CBC模式。需要完整性认证功能时也可选用该模式。
- 容易丢信号的环境,或对明文格式有特殊要求的环境,可选用CFB模式。
- 不易丢信号,但信号特别容易错,且明文冗余特别多,可选用OFB模式。
有限域
AES算法
AES提出的背景
DES算法由于其密钥较短,难以抵抗现有的攻击,因此不再作 为加密标准
AES算法框架和参数说明
设计思想
设计简单
速度快,编码紧凑
抵抗所有已知的攻击
没有采用Feistel结构,轮函数由3个不同的可逆均匀变 换构成的
轮函数
线性混合层->确保多轮之上的高度扩散
非线性层->将具有最优的“最坏情况非线性特性”的S盒并行使用,确保混淆特性
密钥加层->单轮子密钥简单的异或到中间状态上,实现一次性掩盖
结构
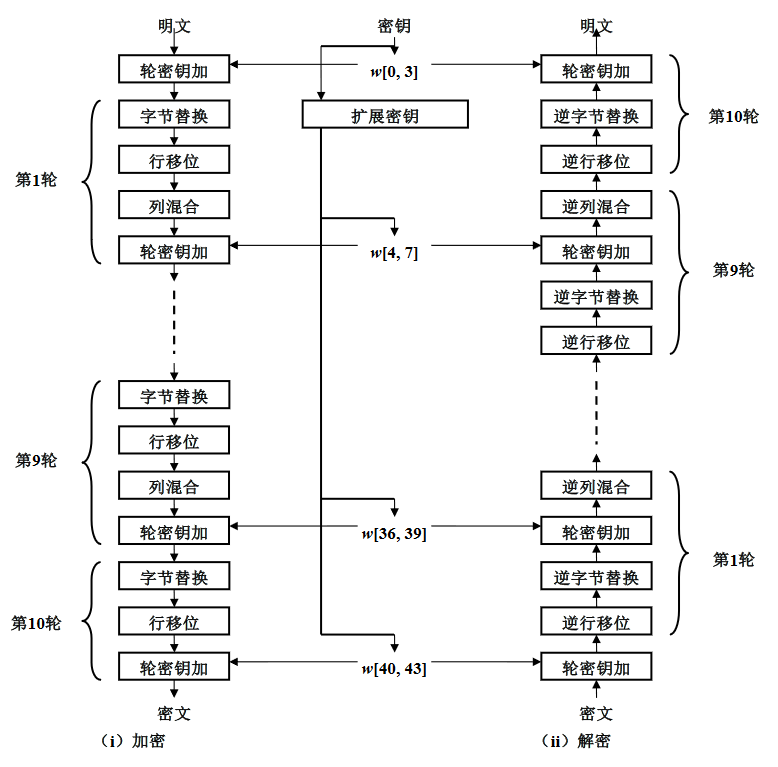
轮函数
字节代换(S盒)
解密用到逆S盒
行移位
状态阵列的各行进行循环移位,不同行的移位量不同
0行:不动
1行:循环左移C1字节
2行:循环左移C2字节
3行:循环左移C3字节
解密则相应逆行移位
列混淆
列混合运算也可写为矩阵乘法
轮密钥加
轮密钥与状态进行逐比特异或
轮密钥由种子密钥通过密钥编排算法得到
轮密钥长度与分组长度相同
AES密钥编排
由密钥扩展和轮密钥选取两部分组成
SM4算法
- SM4是一个分组密码算法,分组长度和密钥长度均为128比特。加密算法与密钥扩展算法都采用32轮非线性迭代结构
整体结构
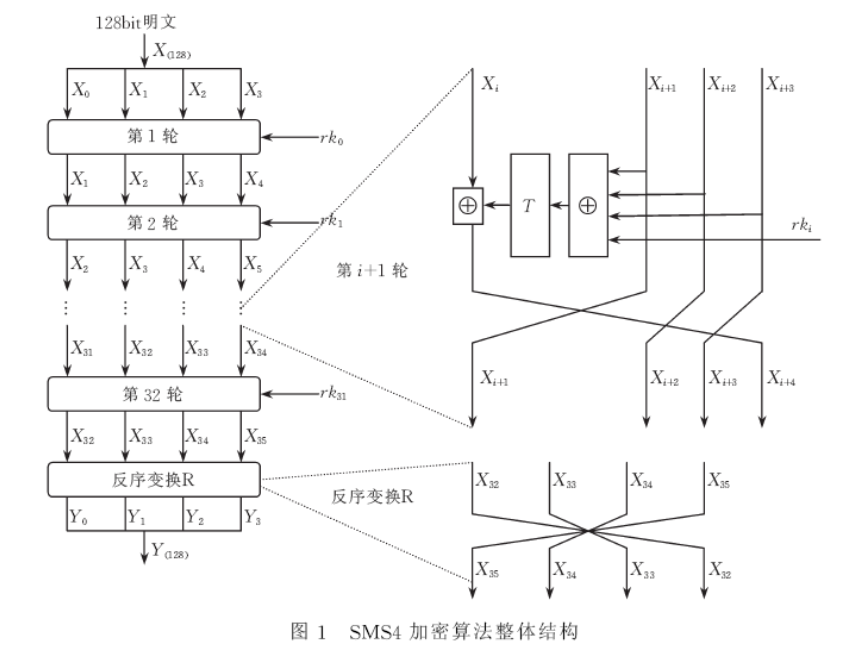
第四章 公钥密码
对称密码的困境
->密钥共享和管理
->不支持“开放系统”
两个没有预先建立关系的用户
公钥密码体制
- 主要思想:从一个方向计算非常容易,而 从另一个方向计算则很困难
公钥密码的理论基础: 陷门单向函数


公钥加密结构
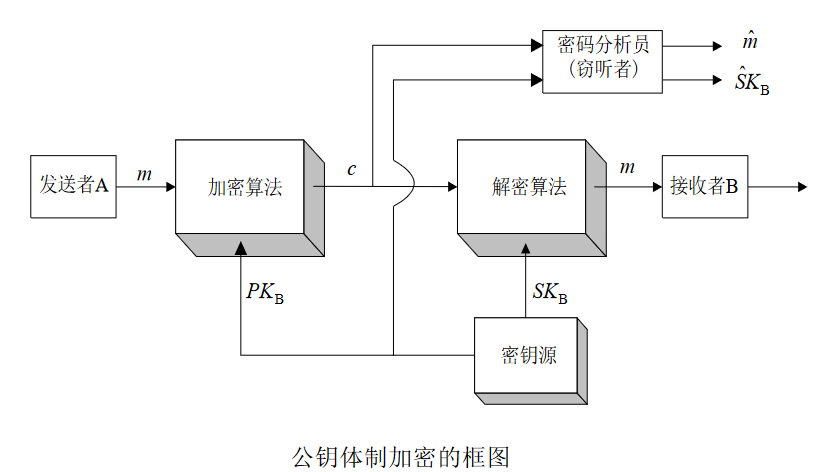
公钥认证结构

公钥密码体制的优势
密钥分发:公钥能够采用公开(认证的)信道进行传输;
密钥管理:在用户N个用户的系统中,每个用户只需安全保管自己的私钥和N-1个 其他用户的公钥。整个系统仅仅需要维护N个公钥;
开放系统:即使是没有预先建立关系的用户也能通过对方的公钥建立安全通信。公钥密码的主要作用
- 公钥加密
- 数字签名
- 基于公钥的密钥分配
公钥密码算法的要求
容易的:
接收方B产生密钥对(PK.B和SK.B)在计算上是容易的。
发方A对消息m加密以产生密文c,即c=E.PKB[m]在计算上是容易的。
收方B用自己的秘密钥对c解密,即m=D.SKB[c]在计算上是容易的。
不可行:
敌手由PKB求SKB在计算上是不可行的。
敌手由密文c和PKB恢复明文m在计算上是不可行的。
研究公钥密码算法就是要找出合适的陷门单向函数。
RSA加密算法
原理
- 选择两个大素数p, q 。
- 计算 m=pq, z=(p-1)(q-1) 。
- 随机选取 e(其中e<n ), e与z没有公因数。( e, z“互为质数”)
- 选取d使得ed-1能够被z完全整除。 (换言之:ed mod z = 1 )
- 公钥是 (n,e)。私钥是(n,d) 。

加解密过程

例题
RSA的加密、解密过程都为求一个整数的整数次幂,再取模。如果按其 含义直接计算,则中间结果非常大,有可能超出计算机所允许的整数取值 范围。
而用模运算的性质:(a×b) mod n=[(a mod n)×(b mod n)] mod n 就可减小中间结果。
RSA密钥的产生
- 两个大素数p、q的选取。->Miller-Rabin算法
- e的选取和d的计算->选取满足1<e<φ(n)和gcd(φ(n),e)=1的e,并计算满足d·e≡1 mod φ(n)的d。这一问题可由推广的Euclid算法完成。
RSA的安全性
RSA的安全性是基于分解大整数的困难性假定
RSA是确定性的加密算法, 不能抵御选择密文攻击。
几个困难问题
- 大整数分解问题(factorization problem)
- 离散对数问题(discrete logarithm problem)
- 多项式求根问题
- 二次剩余问题(quadratic residue problem)
- 背包问题(knapsack problem)
ElGamal公钥密码体制
Elgamal加密基于CDH假设的单向性
ElGamal公钥密码体制历史
ElGamal公钥加密体制原理

特点:
- 安全性基于有限域上的离散对数的难解性
- 加密算法是概率算法
- 不能抵御选择密文攻击
- 存在密文扩张
ElGamal密码的安全性
参数要求:p应为150位以 上十进制数,500位以上的 二进制数,p-1应有大素数因子。
K必须保密而且必须是一次性的。
ElGamal与RSA的区别
- RSA:大整数分解问题
- ElGamal:循环群的离散对数问题
椭圆曲线密码
椭圆曲线密码体制ECC(elliptic curve cryptography)可用短得多的密钥获得同样的安全性
原理
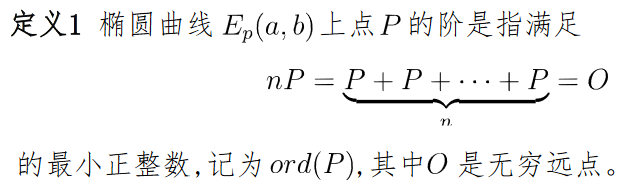

加密流程


优点
- 安全性高
- 密钥量小->在实现相同的安全性能条件下,椭圆曲线密码 体制所需的密钥量远比基于有限域上的离散对数问题的公钥体制的密钥量小
- 灵活性好
SM2椭圆曲线公钥密码加密算法
算法简介
中国商用公钥密码标准算法
一组椭 圆曲线密码算法,其中包含加解密算法、数字签名算法
安全性都是基于求解椭圆曲线上的离散对数问题的困难性
算法原理
密钥产生

加密算法

加密流程图
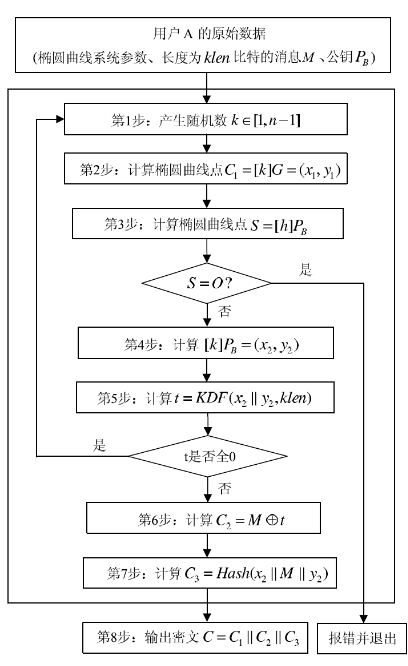
解密算法

解密流程图
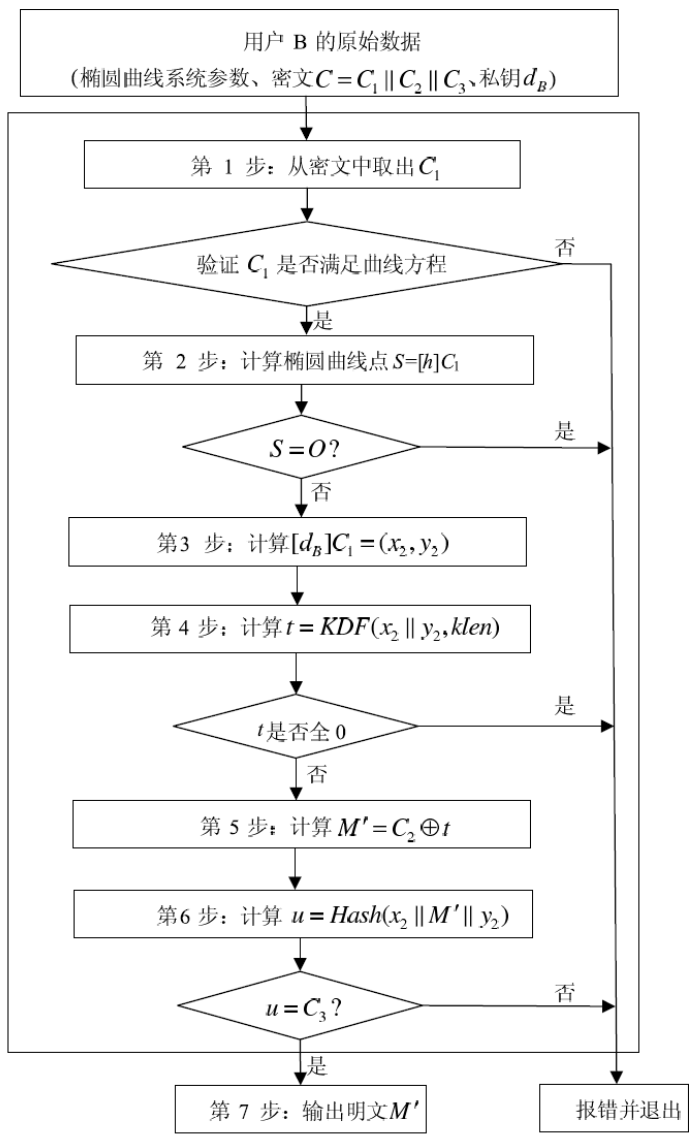
SM2与ECC的区别
ECC算法通常采用NIST等国际机构建议的曲线及参数
SM2算法 的参数需要利用一定的算法产生->更安全
在ECC算法中,用户可以选择MD5、SHA-1等国际通用的哈希算法
SM2算法中则使用SM3哈希算法
SM的优点:解密算法中的检错
第五章 哈希函数
哈希函数的基本概念
定义
将任意长的消息M映射为较短的、固定长度的一个值H(M)。
Hash函数也称为哈希函数、散列函数、压缩函数、杂凑函数、 指纹函数等
其函数值H(M)为哈希值、散列值、杂凑码、指 纹、消息摘要等
目的
Hash函数的目的是为需认证的数据产生一个“指纹”
要求
输入可以是任意长
输出是固定长
易于在软件和硬件实现
安全条件
- 单向性
- 抗弱碰撞性
- 抗强碰撞性
->三者有包含关系,满足后者即可满足前者
生日攻击
第一类生日攻击
问题:“已知一杂凑函数H有n个可能的输出,H(x)是一个特定的输出,如果对H 随机取k个输入,则至少有一个输入y使得H(y)=H(x)的概率为0.5时,k有多大?”
对杂凑函数H寻找上述y的攻击为第I类生日攻击
H(y)=H(x)的概率是1/n <=> H(y)≠H(x)的概率是1-1/n
y取k个随机值得到函数的k个输出中,至少有一个等于H(x)的概率为1-[1-1/n]^k (约等于k/n)
若使上述概率等于0.5,则k=n/2。如果H的输出为m比特长,即可 能的输出个数n=2m,则k=2^(m-1)
生日悖论
问题描述:“在k个人中至少有两个人的生日相同的概率大于0.5时,k至少多大?”
设有k个整数项,每一项都在1到n之间等可能地取值。
P(n, k):k个整数项中至少有两个取值相同的概率
生日悖论就是求使得P(365,k)≥0.5的最小k
P(365,23)=0.5073,即只需23人
之所以称这一问题是悖论是因为: 当人数k给定时,得到的至少有两个人的生日相同的概率比想象的要大得多
生日悖论推广问题

令P(n, k)>0.5,可得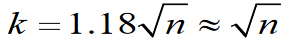
第二类生日攻击
寻找函数H的具有相同输出的两个任意输入的攻击方式。
应用
输出长度与碰撞->生日攻击给出了消息摘要长度的下界
通常建议消息摘要的最小可接受的长度为128比特
SHA-1密码杂凑函数
MD5哈希算法
输入:任意长的消息(图中为K比特)
分组:512比特
输出:128比特的消息摘要。
安全杂凑算法SHA-1
安全哈希算法(Secure Hash Algorithm, SHA)
输入:小于264比特长的任意消息,分为512比特长的分组。
输出:160比特长的消息摘要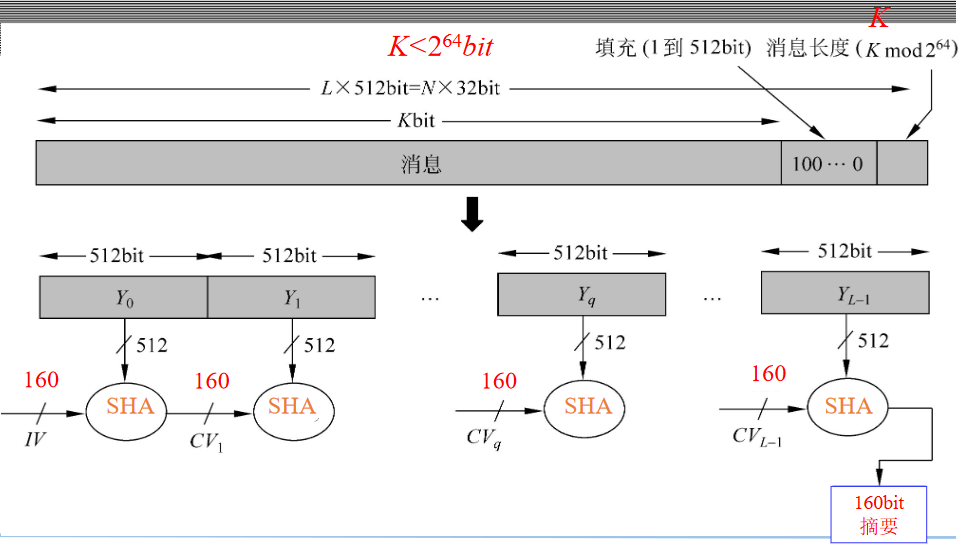
算法处理步骤
1)消息填充
对消息填充,使得其比特长在模512下为448,即填充后消息的长度为 512的某一倍数减64,留出的64比特备用(¥)
该步骤是必须的
填充方式:第1位为1,其后各位皆为0
2)附加消息的长度
留出的64比特(¥)来表示消息被填充前的长度
3)对MD缓冲区初始化
使用160比特长的缓冲区存储中间结果和最终杂凑值
缓冲区为5个32比特以big-endian方式存储数据的寄存器(A, B, C, D, E)
分别为A=67452301, B=EFCDAB89, C=98BADCFB, D=10325476, E=C3D2E1F0。
4)以分组为单位对消息进行处理(复杂)
每一分组Yq都经一压缩函数处理,压缩函数由4轮处理 过程构成,每一轮又由20步迭代组成。
第4轮的输出(即第80步迭代的输出)再与第1轮的输 入CV.q相加,以产生CV.(q+1),其中加法是缓冲区5个字中的 每一个字与CV.q中相应的字模2^(32)相加。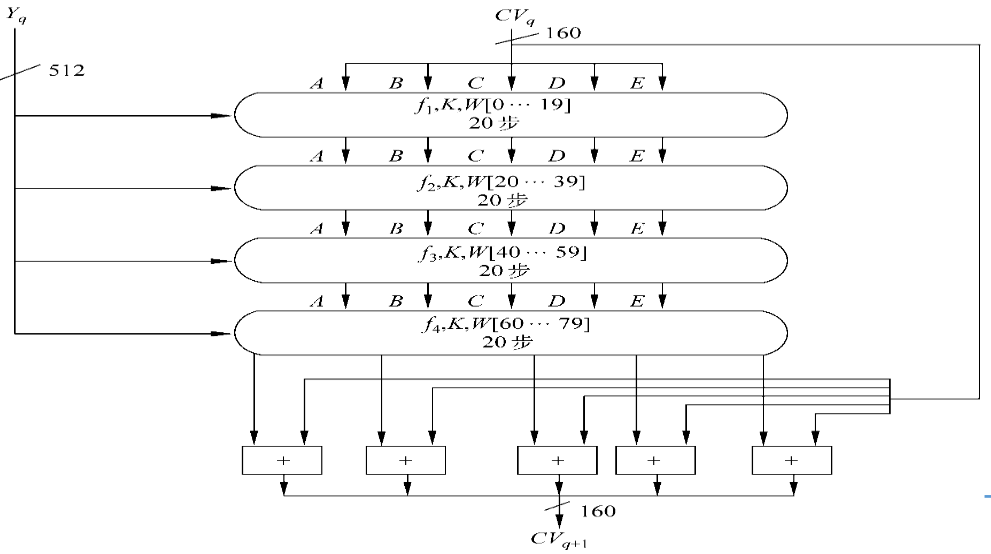
5)输出消息
输出消息的L个分组都被处理完后,最后 一个分组的输出即为160比特的消息摘要。
压缩函数
SHA的压缩函数由4轮处理过程组成,每轮处理过程20步迭代运算组成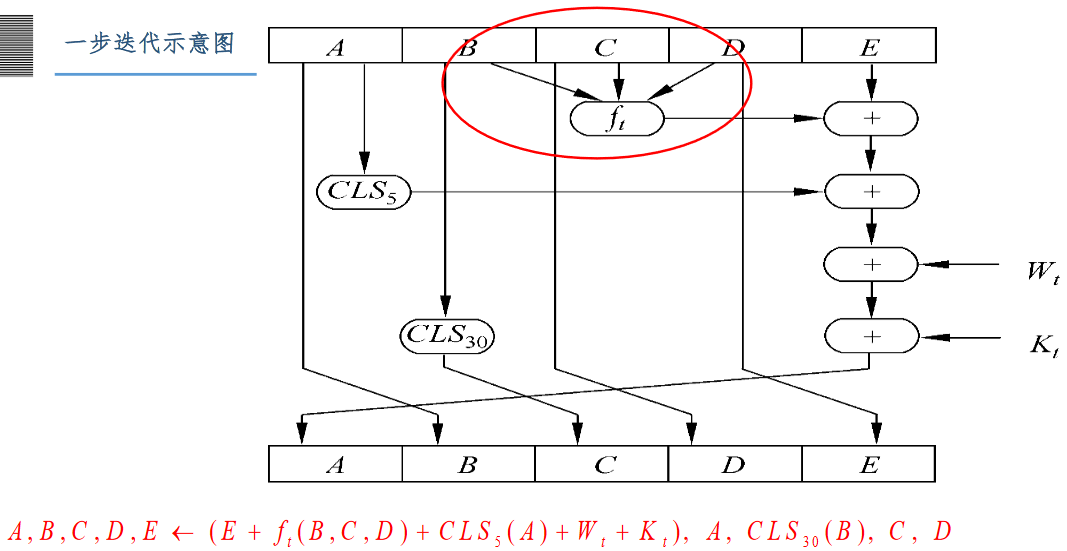
公式解释:
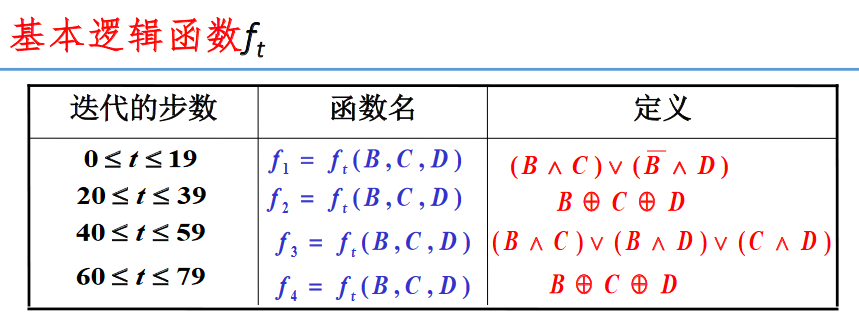
字W.t的产生
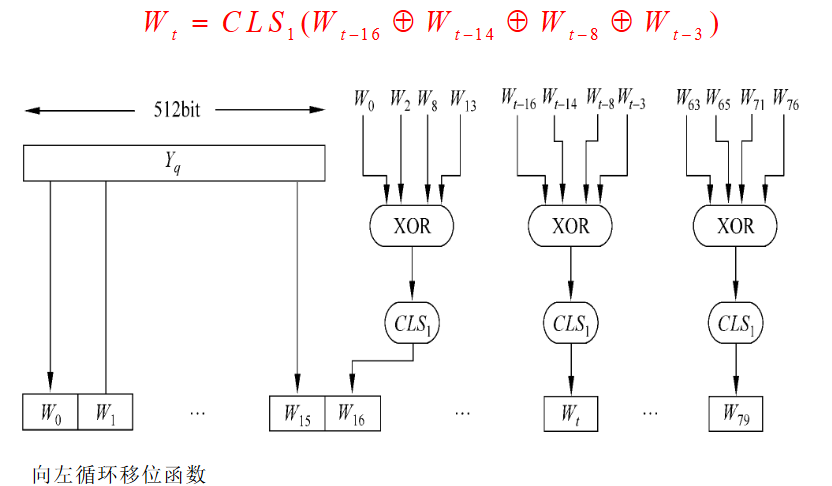
常量字Kt
Kt = 0x5A827999 (0 <= t <= 19)
Kt = 0x6ED9EBA1 (20 <= t <= 39)
Kt = 0x8F1BBCDC (40 <= t <= 59)
Kt = 0xCA62C1D6 (60 <= t <= 79).
SHA系列Hash函数
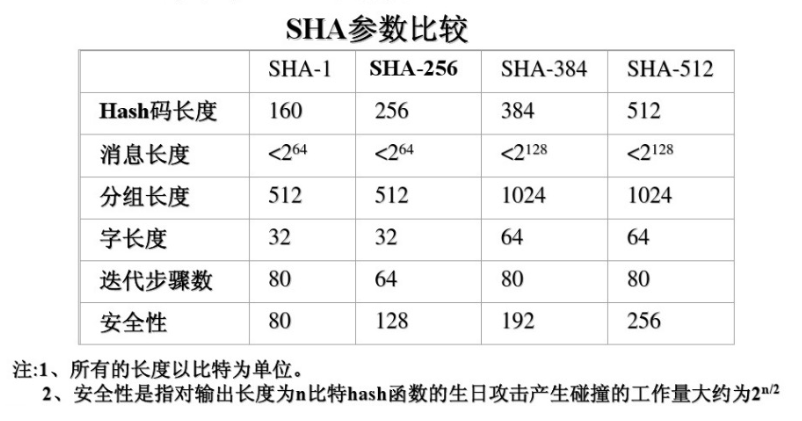
SM3密码杂凑函数
输入:输入:小于264比特长的任意消息
输出:哈希值长度为256比特
常量和函数
IV、T.j为常量
FF.j、GG.j如下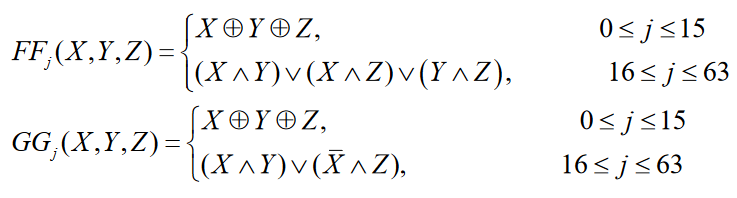
P.0(X)、P.1(X)如下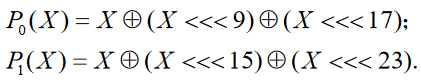
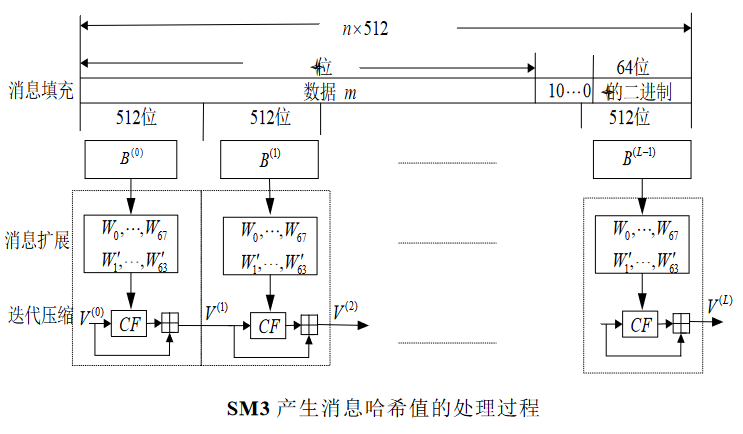
1)数据填充
目的是使填充后的数据长度为512的整数倍
消息 的长度为l比特->
首先将比特“1”添加到m的末尾,再添加k 个“0”,其中k满足l+1+k=448 mod 512
然后再添加一个64位比特串,该比特串是长度l的二进制表示
2)迭代压缩
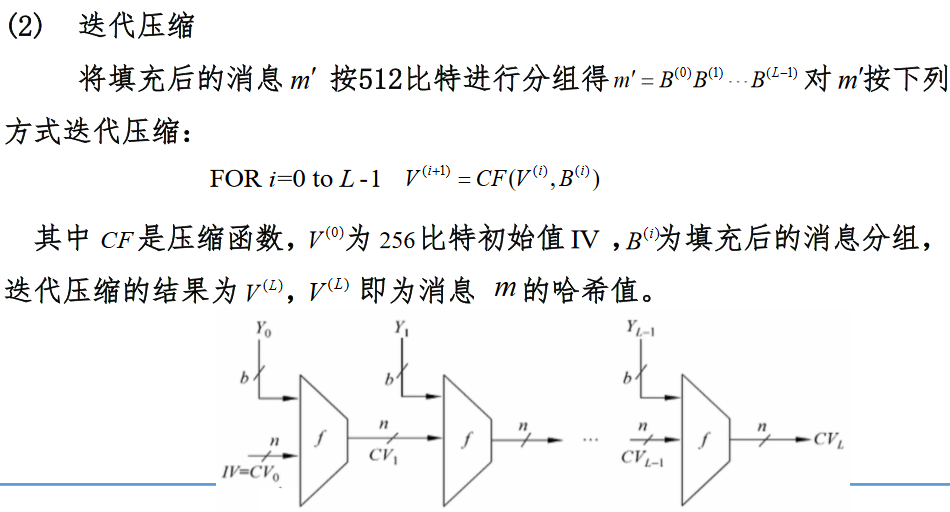
3)消息扩展

->压缩函数

流程图
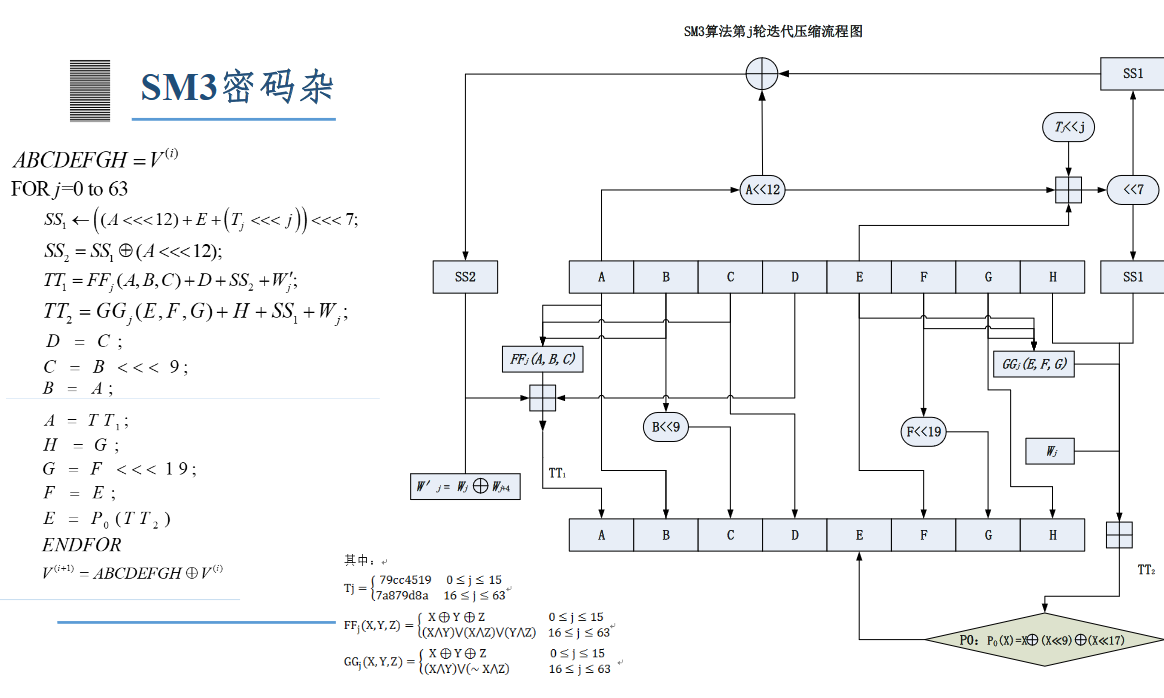
5)输出哈希值
输出256比特的哈希值y=ABCDEFGH
SM3哈希算法的安全性
- FF.j(X,Y,Z)和GG.j(X,Y,Z)是非线性函数,经过循环迭代后提供混淆作用
- 置换函数P.0(X)和P.1(X)是线性函数,经过循环迭代后提供扩散作用
SHA3密码杂凑函数
结构
采用了一种被称为海绵结构(海绵函数)的新的迭代结构
海绵函数允许输入长度和输出长度都可变
在海绵函数中,输入数据被分为固定长度的数据分组。每个分组逐次作为迭代的输入,同时上轮迭代的输出也反馈至下轮的迭代中,最终产生HASH码
特点
- 安全性
可以抵御对Hash函数的现有攻击。
到目前为止,没有发现它有严重的安全弱点。 - 灵活性
可选参数配置,能够适应Hash函数的各种应用。 - 高效性
设计简单,软硬件实现方便。在效率方面,它是高效的。
尚未广泛应用,需要经过实践检验!