FGSM
算法原理
快速梯度符号法(Fast Gradient Sign Method,FGSM)是一种最早的对抗攻击方法之一。其基本思想是通过计算输入图像在损失函数上的梯度,并沿着梯度上升方向对图像进行扰动,从而生成对抗样本。具体公式为:
$$ x_{\text{adv}} = x + \epsilon \cdot \text{sign}(\nabla_x J(\theta, x, y)) $$
其中,$x_{\text{adv}}$ 为对抗样本,$x$为原始输入,$\epsilon$为扰动强度,$\nabla_x J(\theta, x, y)$为损失函数$J$对输入$x$的梯度。
代码实现
FGSM的核心算法在FGSM类中实现,除了初始化方法以外,这个类只有唯一一个函数,即攻击函数attack。这部分在示例代码中已经完成,但之后的攻击算法都基于这一函数实现,因此这里对这一函数进行详细分析,attack函数实现如下:
def attack(self):
perturbed_img=[]
perturbed_label=[]
org_img=[]
org_label=[]
wrong=0
right=0
success=0
for i,(img,label) in enumerate(self.data()):
if i==self.num_size:
break
tensor_img = paddle.to_tensor(img)
tensor_label=paddle.to_tensor(label)
tensor_img.stop_gradient = False
predict = self.model(tensor_img)
pred=predict.argmax(axis=1)
if pred == tensor_label:#如果被正确分类则执行攻击
right+=1
loss = self.criterion(predict, tensor_label)
loss.backward()
grad = paddle.to_tensor(tensor_img.grad)
grad = paddle.sign(grad)
adv_img = tensor_img + self.epsilon * grad
#攻击完成之后再次预测
predict = self.model(adv_img)
pred=predict.argmax(axis=1)
if pred!=tensor_label:
success+=1
#将攻击后的图片保存下来
adv_img=paddle.transpose(adv_img,perm=[0,2,3,1]).numpy()
tensor_img=paddle.transpose(tensor_img,perm=[0,2,3,1]).numpy()
adv_img=np.squeeze(adv_img)
tensor_img=np.squeeze(tensor_img)
adv_img=adv_img*127.5+127.5
tensor_img=tensor_img*127.5+127.5
adv_img=adv_img.astype(np.int64)
perturbed_img.append(adv_img)
tensor_img=tensor_img.astype(np.int64)
org_img.append(tensor_img)
org_label.append(tensor_label.numpy())
perturbed_label.append(pred.numpy())
else:
wrong+=1
continue
if right:
succ_rate=success/right
else :
print("全都预测错误")
return
print(right)
return succ_rate,perturbed_img,org_img,perturbed_label,org_label
这一函数定义了一些初始变量,然后遍历数据图片,首先将图片输入模型以获取分类结果,对正确分类的图片进行攻击,计算损失,然后反向传播计算梯度,获取梯度符号后计算对抗样本,在图片上添加对抗样本。然后将对抗图片输入模型重新预测,比较预测结果与真实标签,并进行结果计数。然后保存结果,将攻击后的图片和原始图片进行转置、去除维度、反归一化、类型转换等处理后再保存到相应列表,根据结果计数来计算攻击成功率并返回。
返回结果分别为攻击成功率、攻击后图片、原始图片、攻击后分类标签、原始分类标签。这里的攻击成功率succ_rate由两个计数变量right和success计算得出,其中right是原始模型分类正确的图片数,success是原本分类正确而攻击后分类错误的图片数,攻击成功率计算公式为succ_rate=success/right。
运行测试
接下来进行效果测试,这里的模型(model)为vgg16,损失函数为交叉熵损失,批大小(batch size)为1,扰动大小设为4,数据量为1000,运行结果如下:

FGSM方法的攻击成功率约为73.4%,运行时间为57秒左右。
使用示例代码对攻击结果进行可视化,如下:
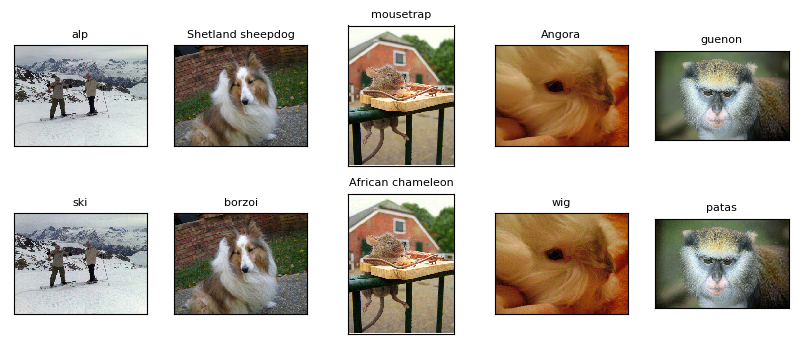
上图中第一行为原始图片及正确分类结果,而第二行为攻击后图片及攻击后分类结果。
BIM
算法原理
基本迭代法(Basic Iterative Method, BIM)是快速梯度符号法(FGSM)的扩展版本。它通过在每一步迭代中对输入图像进行小幅度扰动,从而生成更具欺骗性的对抗样本。与FGSM不同,BIM通过多次迭代累积梯度,从而在每一步扰动中逐渐增强对抗效果。BIM的公式为:
$$
x^{(n+1)}{\text{adv}} = \text{clip}{x, \epsilon} \left{ x^{(n)}{\text{adv}} + \alpha \cdot \text{sign}(\nabla{x^{(n)}{\text{adv}}} J(\theta, x, y)) \right}
$$
其中, $x^{(n)}{\text{adv}}$ 表示第$n$次迭代后的对抗样本,$\alpha$ 为每一步的扰动大小, $\epsilon$为总扰动范围,$\text{clip}$操作用于确保对抗样本在合法范围内。
代码实现
以下是BIM的代码实现的核心部分,与FGSM相比,主要的不同之处在于多次迭代和每次迭代中的裁剪操作。
if pred== tensor_label:#如果被正确分类则执行攻击
right+=1
# Add code
for iter in range(self.num_iters):# 多次迭代
adv_img.stop_gradient = False
predict=model(adv_img)
loss = self.criterion(predict, tensor_label)
for parameter in self.model.parameters():
parameter.clear_grad()
loss.backward(retain_graph=True)
grad = paddle.to_tensor(adv_img.grad)
delta = self.alpha * paddle.sign(grad)
tmp_img = adv_img + delta
tensor_img=paddle.to_tensor(img)
clip_delta = paddle.clip(tmp_img-tensor_img, min=-self.epsilon, max=self.epsilon)
adv_img=adv_img+clip_delta
#攻击完成之后再次预测
predict = self.model(adv_img)
pred=predict.argmax(axis=1)
if pred!=tensor_label:
success+=1
#将攻击后的图片保存下来
adv_img=paddle.transpose(adv_img,perm=[0,2,3,1]).numpy()
tensor_img=paddle.transpose(tensor_img,perm=[0,2,3,1]).numpy()
adv_img=np.squeeze(adv_img)
tensor_img=np.squeeze(tensor_img)
adv_img=adv_img*127.5+127.5
tensor_img=tensor_img*127.5+127.5
adv_img=adv_img.astype(np.int64)
perturbed_img.append(adv_img)
tensor_img=tensor_img.astype(np.int64)
org_img.append(tensor_img)
org_label.append(tensor_label.numpy())
perturbed_label.append(pred.numpy())
break# 成功的退出迭代
#end addcode
BIM实际上是FGSM的迭代版本,依据FGSM方法获取对抗样本并添加,在每次迭代后进行clip操作以控制扰动强度,在每次迭代后进行分类预测,如果成功则退出迭代,或者达到最大迭代次数自动退出。
运行测试
接下来进行效果测试,这里的模型(model)同样为vgg16,损失函数为交叉熵损失,批大小(batch size)为1,扰动大小设为4,数据量为1000,运行结果如下:

FGSM方法的攻击成功率约为90.6%,运行时间为1分26秒左右。
使用示例代码对攻击结果进行可视化,如下:

上图中第一行为原始图片及正确分类结果,而第二行为攻击后图片及攻击后分类结果。
PGD
算法原理
投影梯度下降法(Projected Gradient Descent, PGD)是BIM的一个扩展版本,它被认为是最有效的第一阶对抗攻击方法之一。PGD方法通过多次迭代,在每一步应用FGSM生成扰动,然后将扰动结果投影回合法的输入范围。具体来说,PGD可以看作是带有投影操作的BIM方法。PGD的公式如下:
$$ x^{(0)}{\text{adv}} = x + \delta, \quad \delta \sim \mathcal{U}(-\epsilon, \epsilon) \ x^{(n+1)}{\text{adv}} = \text{clip}{x, \epsilon} \left{ x^{(n)}{\text{adv}} + \alpha \cdot \text{sign}(\nabla_{x^{(n)}_{\text{adv}}} J(\theta, x, y)) \right} $$
其中,$x^{(0)}{\text{adv}}$是初始对抗样本,通过在原始输入上添加一个均匀分布的随机噪声$\delta$生成。每一步迭代通过在当前对抗样本上添加扰动$\alpha \cdot \text{sign}(\nabla{x^{(n)}_{\text{adv}}} J(\theta, x, y))$,并使用$\text{clip}$操作将结果投影回合法范围$[x - \epsilon, x + \epsilon]$。
代码实现
以下是PGD的代码实现的核心部分,与BIM相比,PGD在初始时添加了一个随机噪声,并且每一步都包含投影操作。
if pred== tensor_label:#如果被正确分类则执行攻击
right+=1
delta_init = paddle.uniform(img.shape, dtype='float32', min=-self.epsilon, max=self.epsilon)
clip_delta = paddle.clip(delta_init, -self.epsilon, self.epsilon)
tensor_img_iter = tensor_img+clip_delta
for iter in range(self.num_iters):
tensor_img_iter.stop_gradient=False
predict=self.model(tensor_img_iter)
loss = self.criterion(predict, tensor_label)
for param in self.model.parameters():
param.clear_grad()
loss.backward(retain_graph=True)
grad = paddle.to_tensor(tensor_img_iter.grad)
delta = self.alpha * paddle.sign(grad)
tensor_img = paddle.to_tensor(img)
tmp_img = tensor_img_iter+delta
clip_delta = paddle.clip(tmp_img-tensor_img, min=-self.epsilon, max=self.epsilon)
adv_img = tensor_img_iter+clip_delta
#攻击完成之后再次预测
predict = self.model(adv_img)
pred = predict.argmax(axis=1)
if pred != tensor_label:
success += 1
#将攻击后的图片保存下来
adv_img = paddle.transpose(adv_img,perm=[0,2,3,1]).numpy()
# tensor_img = paddle.to_tensor(img)
tensor_img = paddle.transpose(tensor_img,perm=[0,2,3,1]).numpy()
adv_img = np.squeeze(adv_img)
tensor_img = np.squeeze(tensor_img)
adv_img = adv_img*127.5+127.5
tensor_img = tensor_img*127.5+127.5
adv_img = adv_img.astype(np.int64)
perturbed_img.append(adv_img)
tensor_img = tensor_img.astype(np.int64)
org_img.append(tensor_img)
org_label.append(tensor_label.numpy())
perturbed_label.append(pred.numpy())
break
tensor_img_iter = adv_img
相比BIM,PGD方法的改进主要体现在初始随机噪声的引入,而随机噪声的生成方法,对攻击效果和速度都有明显的影响,这里尝试多种随机噪声生成方法。
均匀分布:
delta_init = paddle.uniform(img.shape, dtype='float32', min=-self.epsilon, max=self.epsilon)
高斯分布:
delta_init = paddle.normal(shape=img.shape, mean=0.0, std=self.epsilon)
随机分布
delta_init = paddle.rand(shape=img.shape) * self.epsilon
这些生成方法各自具有特点,在运行测试部分测试它们的效果并进行对比分析。
运行测试
以下进行了三次运行测试,分别为均匀分布、高斯分布和随机分布的测试结果,最大迭代次数(num_iter)均设置为5:
均匀分布:

高斯分布:

随机分布:

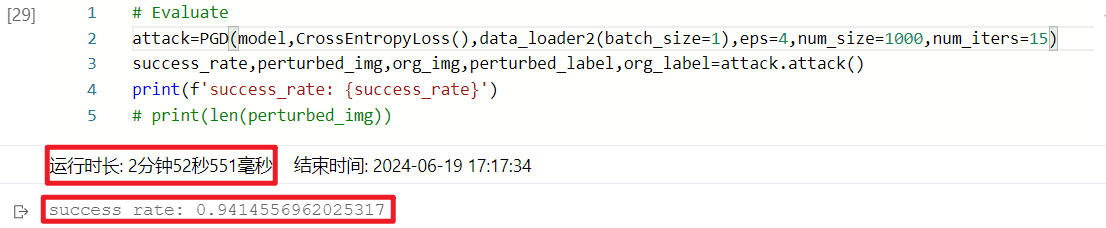
在最大迭代次数设置为5时,均匀分布运行速度最快,而随机分布的攻击成功率最高。但通过与BIM方法的结果对比,这一系列攻击测试的成功率明显偏低,在80%-83%左右,与预期不符,推测是由于最大迭代次数设置得过小,攻击方法尚未收敛,于是将最大迭代次数(num_iter)调整为15,进行重复测试,结果分别如下:
均匀分布:

高斯分布:
随机分布:
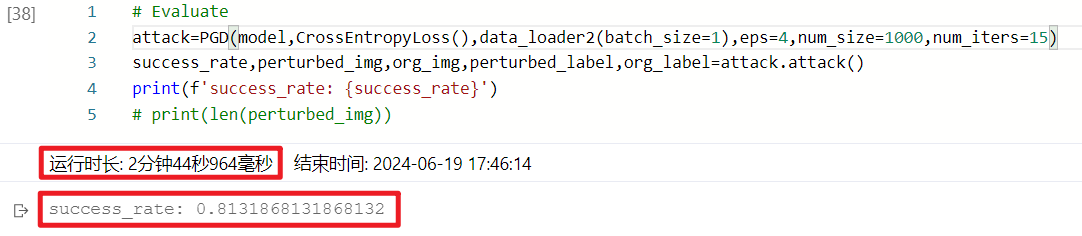
可以看到,均匀分布和高斯分布的攻击成功率均有明显提高,达到了94%以上,但随机分布的攻击成功率反而有所下降。结合上面的测试结果,均匀分布生成随机噪声的PGD方法总体表现最好,高斯分布其次,而随机分布方法受到随机性影响,稳定性较差。同时,相较BIM方法,PGD攻击达到收敛所需的迭代次数更多,应设置更大的最大迭代次数以确保收敛,因此耗费的计算资源和时间也更多,但其攻击成功率也有相应的提升。
将以上不同噪声生成方法在不同最大迭代次数下运行所用的时间及其最终攻击成功率作成柱状图,以供直观地比较不同噪声生成方法的性能差异,如下图:

MIFGSM
算法原理
MIFGSM(Momentum Iterative Fast Gradient Sign Method)是一种改进的对抗攻击方法,基于FGSM的基础,通过引入动量项来加速收敛和提高攻击的稳定性。与传统的FGSM(Fast Gradient Sign Method)相比,MIFGSM在每次迭代中积累梯度信息,从而更有效地找到对抗样本。
MIFGSM 是一种利用动量加速收敛的对抗攻击方法。迭代过程如下:
对于$t = 1$到$T$(迭代次数),首先计算损失相对于输入的梯度:$\nabla_{\mathbf{x}^\mathrm{adv}{t-1}} J(\mathbf{x}^\mathrm{adv}{t-1}, y_{true})$
使用动量累积梯度:$\mathbf{g}t = \alpha \cdot \mathbf{g}{t-1} + \frac{\nabla_{\mathbf{x}^\mathrm{adv}{t-1}} J(\mathbf{x}^\mathrm{adv}{t-1}, y_{true})}{|\nabla_{\mathbf{x}^\mathrm{adv}{t-1}} J(\mathbf{x}^\mathrm{adv}{t-1}, y_{true})|_1}$
使用这一公式更新对抗样本:$\mathbf{x}^\mathrm{adv}t = \mathrm{clip}(\mathbf{x}^\mathrm{adv}{t-1} + \mathrm{clip}(\alpha \cdot \mathrm{sign}(\mathbf{g}_t), -\epsilon, \epsilon), \mathbf{x} - \epsilon, \mathbf{x} + \epsilon)$
代码实现
MIFGSM的代码核心实现如下,与FGSM的区别主要在动量项g的引入并利用其来累计梯度。
if pred == tensor_label:#如果被正确分类则执行攻击
right+=1
# Add code
g = 0#动量初始化
for iter in range(self.num_iters):
adv_img.stop_gradient=False
predict = self.model(adv_img)
loss = self.criterion(predict, tensor_label)
for param in self.model.parameters():
param.clear_grad()
loss.backward(retain_graph=True)
grad = paddle.to_tensor(adv_img.grad)
g = g * self.decay_factor + grad / paddle.norm(grad,p=1)#使用动量累积梯度
delta = self.alpha * paddle.sign(g)
tensor_img = paddle.to_tensor(img)
tmp_img = adv_img + delta
clip_delta = paddle.clip(tmp_img - tensor_img, -self.epsilon, self.epsilon)
adv_img = adv_img + clip_delta
#攻击完成之后再次预测
predict = self.model(adv_img)
pred = predict.argmax(axis = 1)
if pred != tensor_label:
success += 1
#将攻击后的图片保存下来
adv_img = paddle.transpose(adv_img,perm=[0,2,3,1]).numpy()
tensor_img = paddle.transpose(tensor_img,perm=[0,2,3,1]).numpy()
adv_img = np.squeeze(adv_img)
tensor_img = np.squeeze(tensor_img)
adv_img = adv_img*127.5+127.5
tensor_img = tensor_img*127.5+127.5
adv_img = adv_img.astype(np.int64)
perturbed_img.append(adv_img)
tensor_img = tensor_img.astype(np.int64)
org_img.append(tensor_img)
org_label.append(tensor_label.numpy())
perturbed_label.append(pred.numpy())
break
# end addcode
相比FGSM,MIFGSM在开始攻击之初引入了动量项g,根据动量累积公式更新g的值,然后再更新delta;同时MIFGSM也是一个迭代方法,动量项g会在每次迭代中更新,同时也保留了上一次循环的信息。
运行测试
接下来进行效果测试,这里的模型(model)为vgg16,损失函数为交叉熵损失,批大小(batch size)为1,扰动大小设为4,最大迭代次数(num_iters)为5,数据量为1000,衰减因子(decay_factor)为1,运行结果如下:

MIFGSM方法的攻击成功率约为86.6%,运行时间为1分36秒左右。
使用示例代码对攻击结果进行可视化,如下:

上图中第一行为原始图片及正确分类结果,而第二行为攻击后图片及攻击后分类结果。
对比分析
为了横向对比四个攻击方法的性能差异,将同样超参数下的攻击数据作成如下表格,最大迭代次数均为5,如下表:
| 攻击方法 | 时间 (秒) | 攻击成功率 (%) |
|---|---|---|
| FGSM | 57 | 73.4 |
| BIM | 86 | 90.6 |
| PGD | 87 | 82.8 |
| MIFGSM | 96 | 86.6 |
在本场景下,用时最快的方法为FGSM,用时最久为MIFGSM;攻击成功率最高的方法为BIM,攻击成功率最低的为FGSM。但上述对比不能完全体现方法的优劣,仍需结合具体场景和不同算法的特点选取合适的攻击方法。
首先,FGSM 是一种简单而高效的对抗攻击方法,其优点在于计算速度快,因为只需进行一次梯度计算和一次扰动操作,而它的缺点是生成的对抗样本可能会被防御机制检测出来,因为扰动较大且不一定最优。
BIM 是在FGSM基础上发展而来的迭代攻击方法,相比FGSM具有更高的攻击成功率,但也会增加计算成本和生成时间。其优点在于相对较高的攻击成功率和适应性,可以绕过一些简单的防御机制,但可能需要更多的迭代次数和计算资源。
PGD 是一种更强大的迭代对抗攻击方法,PGD通常可以在较大的扰动范围内找到最优的对抗样本,因此具有较高的攻击成功率。它的缺点在于需要更多的迭代次数和计算成本,尤其是在处理复杂的模型和数据集时。
MIFGSM是基于动量的迭代FGSM方法,MIFGSM在FGSM和PGD之间找到了一种平衡,相比于普通的FGSM,具有更高的攻击成功率,同时相比于PGD,计算成本相对较低。然而,MIFGSM可能需要调节更多的超参数来达到最优效果,并且在处理不同模型和数据集时表现可能有所不同。

